本文对应化学系本科一年级上学期《普通化学原理》和一年级下学期《物理化学》课程的部分内容。

一. 反应级数(Reaction order)

首先引入反应级数的概念，它是化学反应速率方程中，反应物浓度的指数总和。反应级数描述了浓度对反应速率的影响程度。
利用反应级数这个概念，可以将一些常见的化学反应进行分类，如零级反应、一级反应、二级反应等，并对这些反应的动力学进行讨论，下面将进行简单的介绍。

二. 零级反应(Zero-order reaction)

速率方程中，反应物浓度的指数总和为0。此时反应速率与浓度无关。
这是一个没什么讨论空间的反应类型。
例子：表面上发生的非均相反应；底物极大过量时的酶促反应。

这个过程比较好理解。
以酶促反应为例，当底物极大过量时，酶的总量却是有限的。当全部活性位点被底物占据达到饱和状态时，不论如何增加底物浓度，反应速率都不会再进一步上升了。这也对应着米氏动力学(Michaelis–Menten kinetics)曲线右侧的平台区域。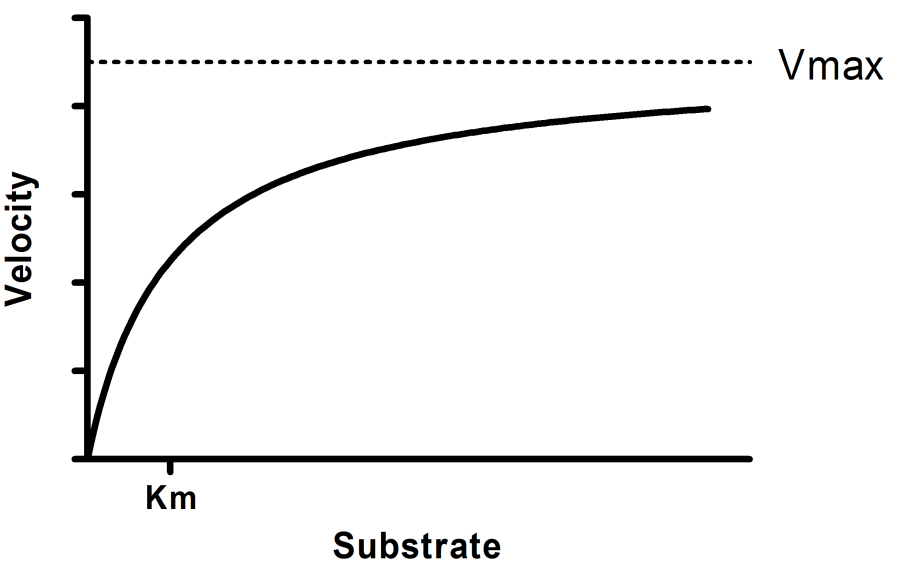

三. 一级反应(First-order reaction)

速率方程中，反应物浓度的指数总和为1。此时反应速率与反应物浓度的一次方成正比。

$$ \text{A} \xrightarrow{k_1} \text{B} $$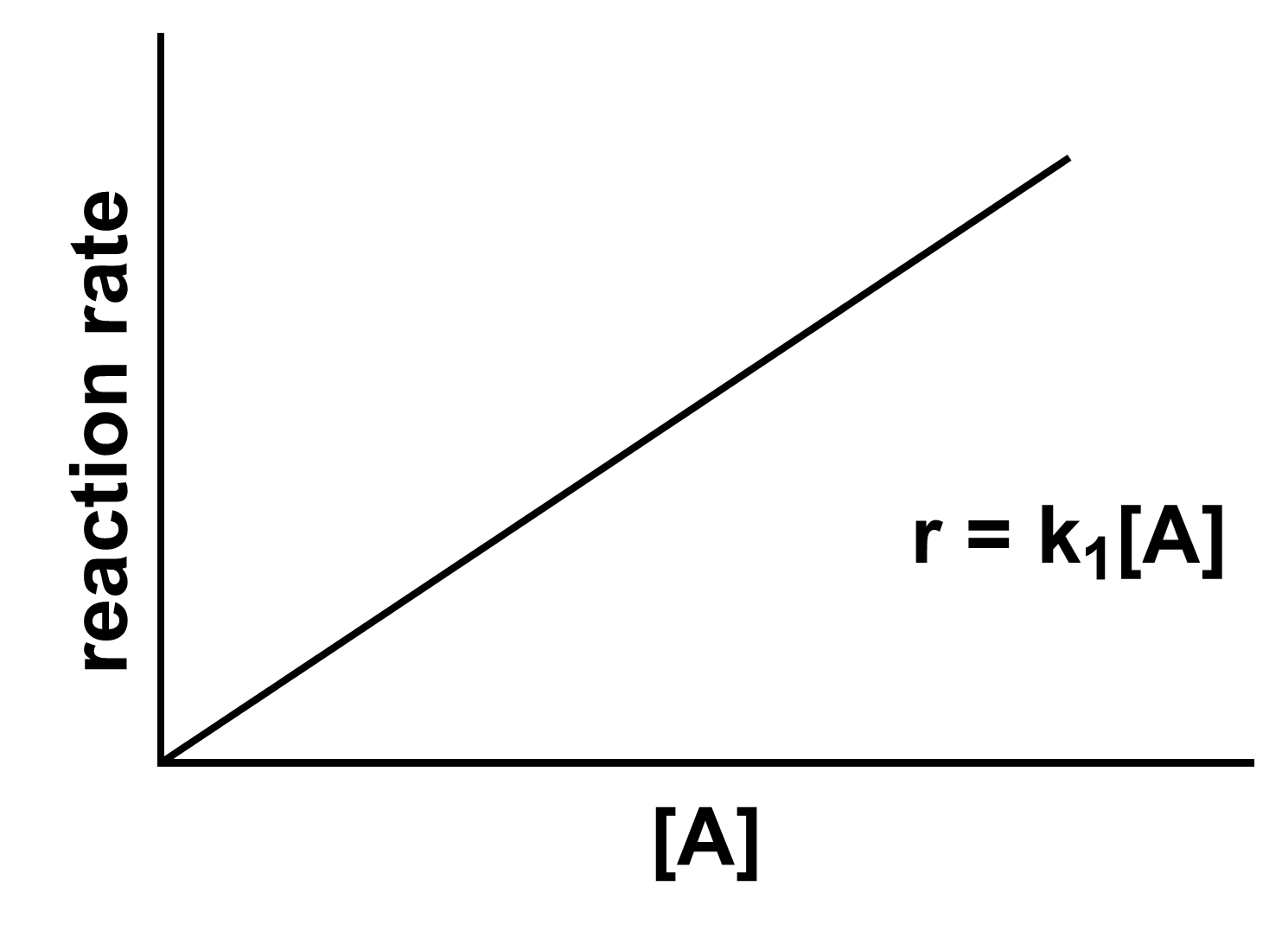

这里的比例系数${k_1}$就是这个反应的速率常数。

一级反应是比较常见的反应类型。
例子：一些分解反应；底物浓度较低时的酶促反应；核素衰变。

还是以酶促反应为例，当底物浓度较低，而酶过量时，活性位点的余量还有很多。新增加的底物都会结合到活性位点，提高反应速率。增加了多少底物，总的反应速率就会相应地、成正比地上升多少。这对应着米氏动力学曲线的左侧的线性区域。

核素的衰变尽管不是化学过程，但是其数学形式是与一级反应是相同的。多出多少核素，反应速率也随之成正比地上升多少。

在日常实验中，尽管我们对反应速率很感兴趣，但是瞬时的反应速率并不容易直接测量，好在物质的浓度是可以通过测吸收或者测荧光发射来迅速测定的。通过测定不同时间点的物质浓度，我们就可以计算出反应速率常数和各个时刻的反应速率。

下面对一级反应的数学形式进行推导，得到物质浓度、反应速率和反应时间之间的关系。

对于反应$$ \text{A} \xrightarrow{k_1} \text{B} $$ 为了便于计算和讨论，我们设
初始时刻 $ t=0 $ 时，反应物$ \text{A} $的浓度为 $[\text{A}]_0 $，生成物$ \text{B} $的浓度为 $ 0 $，
当反应到 $ t=t $ 时，反应物$ \text{A} $的浓度为 $ [\text{A}] $，生成物$ \text{B} $的浓度为 $ [\text{B}] $。

这是个一级反应，所以有
$$ r = -\frac{d[\text{A}]}{dt} = k_1 [\text{A}] $$ 移项后可以获得
$$ \frac{1}{[\text{A}]} d[\text{A}] = -k_1 \, dt $$ 从 $t$ 时刻到 $t_0$ 时刻做个积分
$$ \int_{[\text{A}]_0}^{[A]} \frac{1}{[\text{A}]} d[\text{A}] = - \int_0^t k_1 \, dt $$ 可得到物质浓度与速率常数之间的关系
$$ \ln [\text{A}] - \ln [\text{A}]_0 = -k_1 t $$

对于反应速率常数的计算，比较古典的做派是将$ \text{A} $的浓度取对数，然后对 $t$ 作线性拟合。不过得益于计算机的发展，直接把各个时间点下的$\text{A}$的浓度输入到诸如Prism之类的软件里，使用单相衰减(One phase decay)模型就能完成计算。如果测定的是$\text{B}$的浓度，则是单相衰减(One phase association)模型。不过其实没区别，只是差了个正负号而已。
后面会对使用Prism计算${k_1}$的过程做具体介绍。
参考阅读：
Prism曲线拟合指南 方程：单相衰减
Prism曲线拟合指南 方程：单相结合

对于一级反应，有一个重要的参数是半衰期(Half-life)，它代表反应进行一半所需的时间。

对于前面得到的动力学方程$ \ln [\text{A}] - \ln [\text{A}]_0 = -k_1 t $，整理一下，当反应进行到一半时，有
$$\ln \frac{[\text{A}]}{[\text{A}]_0} = -k_1 t = \frac{1}{2}$$ $$t_{1/2} = \frac{\ln 2}{k_1} = \frac{0.693}{k_1}$$ 可以看到，一级反应的半衰期是由速率常数${k_1}$决定的，与反应物的浓度无关。${k_1}$和半衰期可以说是一级反应的“本征”属性、“内廪”属性。

在讨论放射性同位素时，半衰期是非常重要的参数。

例1：$^{14}\text{C}$可用于古文物测定，其半衰期是5730年。从据说是公元1世纪死海古卷取出的纸片，烧成灰，通过对灰分放射性活度的测定，确认其中$^{14}\text{C}$含量为现在的生物活体的0.795倍，计算古卷的年代。

可先由半衰期计算速率常数，再根据前面推导出的公式计算古文物年代。
$$k_1 = \frac{0.693}{t_{1/2}} = \frac{0.693}{5730} = 1.21 \times 10^{-4} \text{a}^{-1}$$ 根据$\ln \frac{[\text{A}]}{[\text{A}]_0} = -k_1 t$，其中$\frac{[\text{A}]}{[\text{A}]_0}$代表样品与活物中$^{14}\text{C}$含量之比，有
$$\ln 0.795 = -1.21 \times 10^{-4} t$$ 可得 $t$ 约为1900年。古卷是1900年之前的，与传说相吻合。

例2：$^{18}\text{F}$是重要的医用同位素，其半衰期是109.8min。若某时刻$^{18}\text{F-FDG}$的放射性活度为100%，则3h后的活度剩余多少？

想偷懒的话，直接计算3h对应多少个半衰期就好，可得剩余活度为$ \left(\frac{1}{2}\right)^{\frac{180}{109.8}} = 32.11\% $。
也可以像刚才那样规规矩矩地计算。已知
$$ t_{1/2} = \frac{0.693}{k_1} = 109.8 \, \text{min} $$ 在3h后，

$$ \begin{align} \ln \frac{\text{[}^{18}\text{F]}}{\text{[}^{18}\text{F]}_0} &= -k_1 t \\ & = - \frac{t}{t_{1/2}} \cdot 0.693 \\ & = - \frac{180}{109.8} \cdot 0.693 \\ & = -1.136 \end{align} $$

所以$$\frac{[^{18}\text{F}]}{[^{18}\text{F}]_0} = e^{-1.136} = 32.11\%$$

四. 二级反应(Second-order reaction)

速率方程中，反应物浓度的指数总和为2。典型的形式是

$$ \text{A} + \text{B} \xrightarrow{k_2} \text{C}$$

二级反应太常见了，就不举例子了。
对于二级反应的速率测定，我们仍然可以将问题转化为物质浓度的测定。现在的困难在于，多了一个反应物$\text{B}$，而且$\text{A}$和$\text{B}$的浓度还在互相影响，导致问题比较复杂。$$r = - \frac{d[\text{A}]}{dt} = k_2 [\text{A}][\text{B}] $$为了解决这个麻烦，实验上常用的手段是把二级反应做成准一级反应(Pseudo first-order reaction)。
准一级反应的实质仍是二级反应，但某一反应物极大过量，使反应的速率曲线趋向于一级反应速率曲线。
在中文资料中，对pseudo一词的翻译不尽相同，所以会出现“假一级反应”“拟一级反应”“伪一级反应”之类的各种各样的称呼，但实际上都指的是一个东西。

对于准一级反应，当$\text{B}$极大过量时，$[\text{B}]$近似为一不变的常量，所以有

$$ \begin{align} r = - \frac{d[\text{A}]}{dt} = k_2 [\text{B}][\text{A}] & = k_1 [\text{A}] \quad \Rightarrow \quad \text{pseudo first order reaction} \\ & = k_{\text{obs}}[\text{A}] \\ \end{align} $$

其中
$$k_1 = k_2 [\text{B}] = k_{\text{obs}}$$这里的${k_1}$就是准一级反应的速率常数。它是我们可以通过与一级反应类似的实验设计直接测定出来的速率常数，因此也叫$k_{\text{obs}}$，即表观速率常数(Observed rate constants)。
${k_1}$是真实测得的，但是${k_1}$显然受到$\text{B}$的浓度的影响。
这很好理解，虽然$\text{B}$极大过量，但是它的浓度越高，整体反应速率肯定也越快。
对于某个二级反应，${k_1}$是可变的，而${k_2}$才是它的所谓的“本征”属性、“内廪”属性。
还好，通过测定在不同浓度的$\text{B}$下的${k_1}$，我们可以通过线性拟合，求得${k_2}$。

例：化合物DBD-Cl可以与谷胱甘肽(GSH)反应。DBD-Cl和谷胱甘肽都没有荧光，但产物具有荧光。试测定此反应的动力学参数。

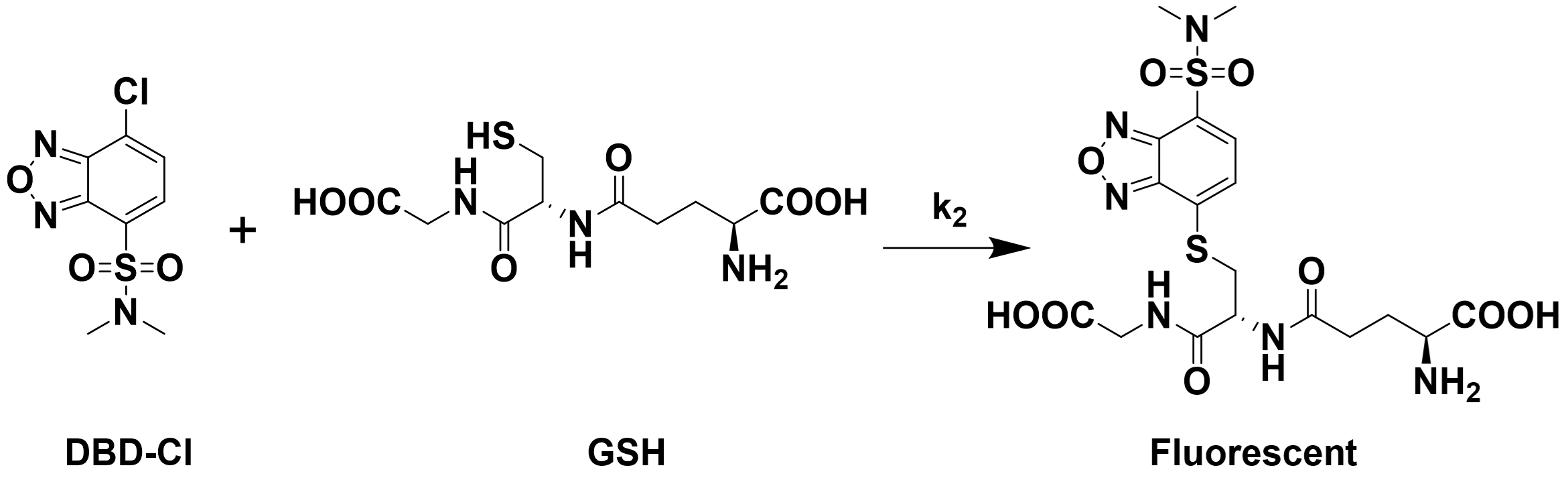
在这个反应中，GSH较易获取，故使GSH极大过量。
固定DBD-Cl的浓度为10μM，设置GSH的浓度分别为100μM，250μM，500μM和1000μM，测定不同GSH浓度下的产物荧光随时间的变化，得到$k_{\text{obs}}$，最终拟合得到${k_2}$。

使用荧光分光光度计完成测定，然后将数据粘贴进Prism。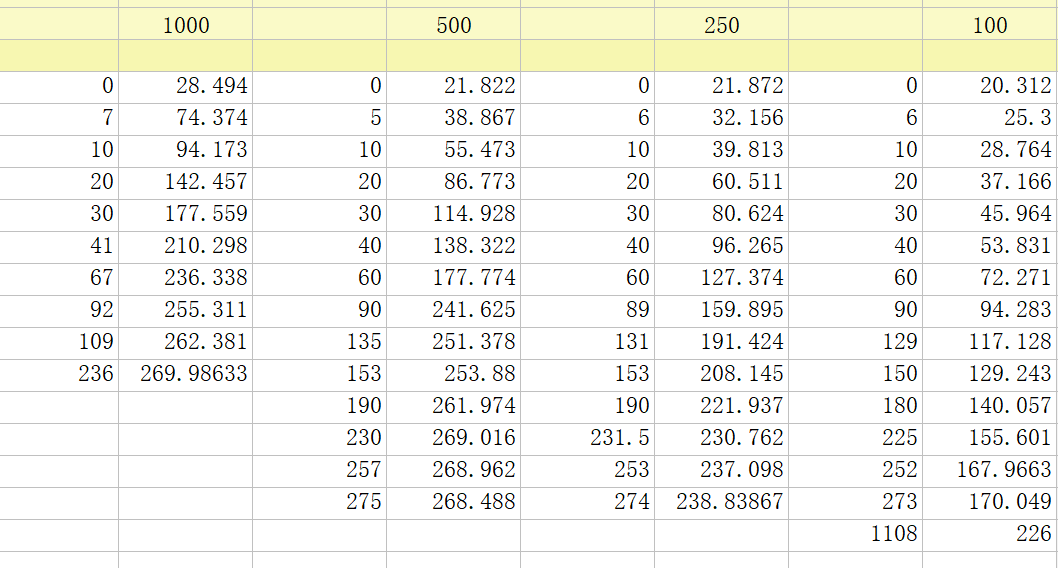

在Prism中进行数据拟合，Analysis → Nonlinear regression → Exponential → One Phase Association，就可以得到不同GSH浓度下的$k_{\text{obs}}$了。

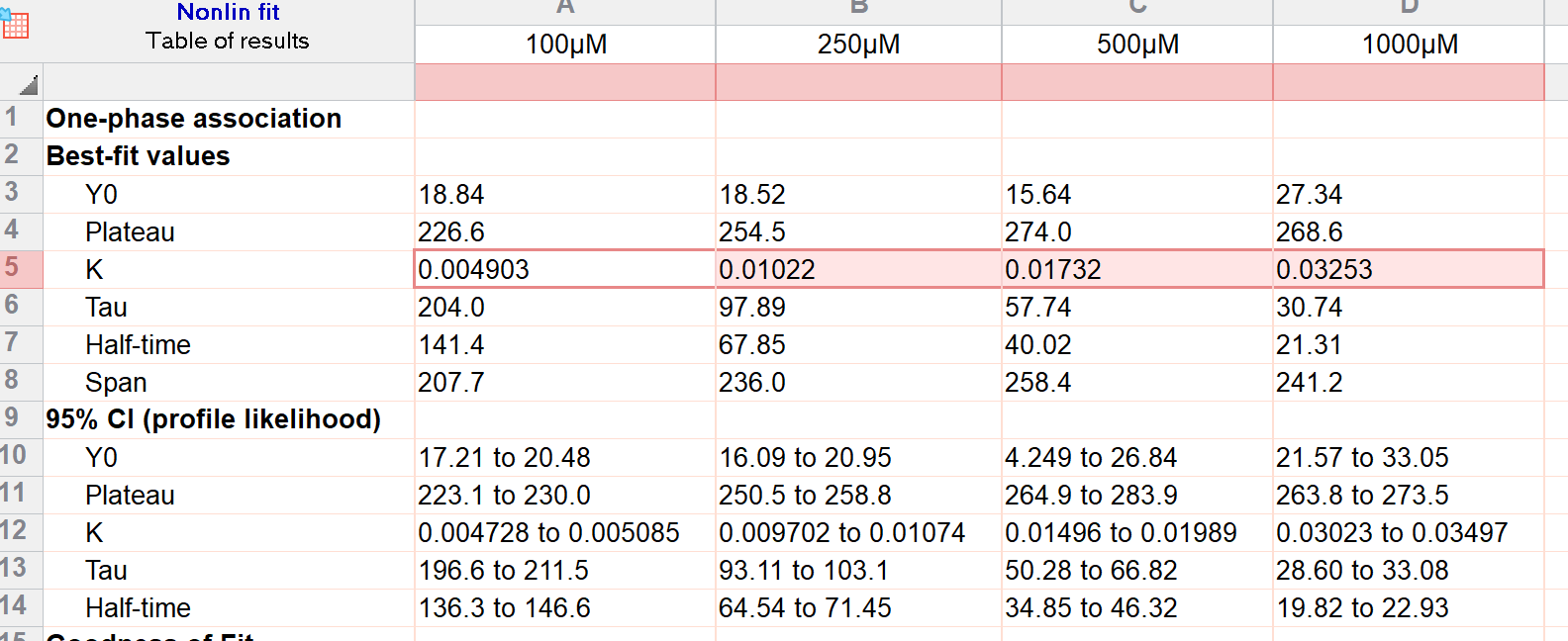
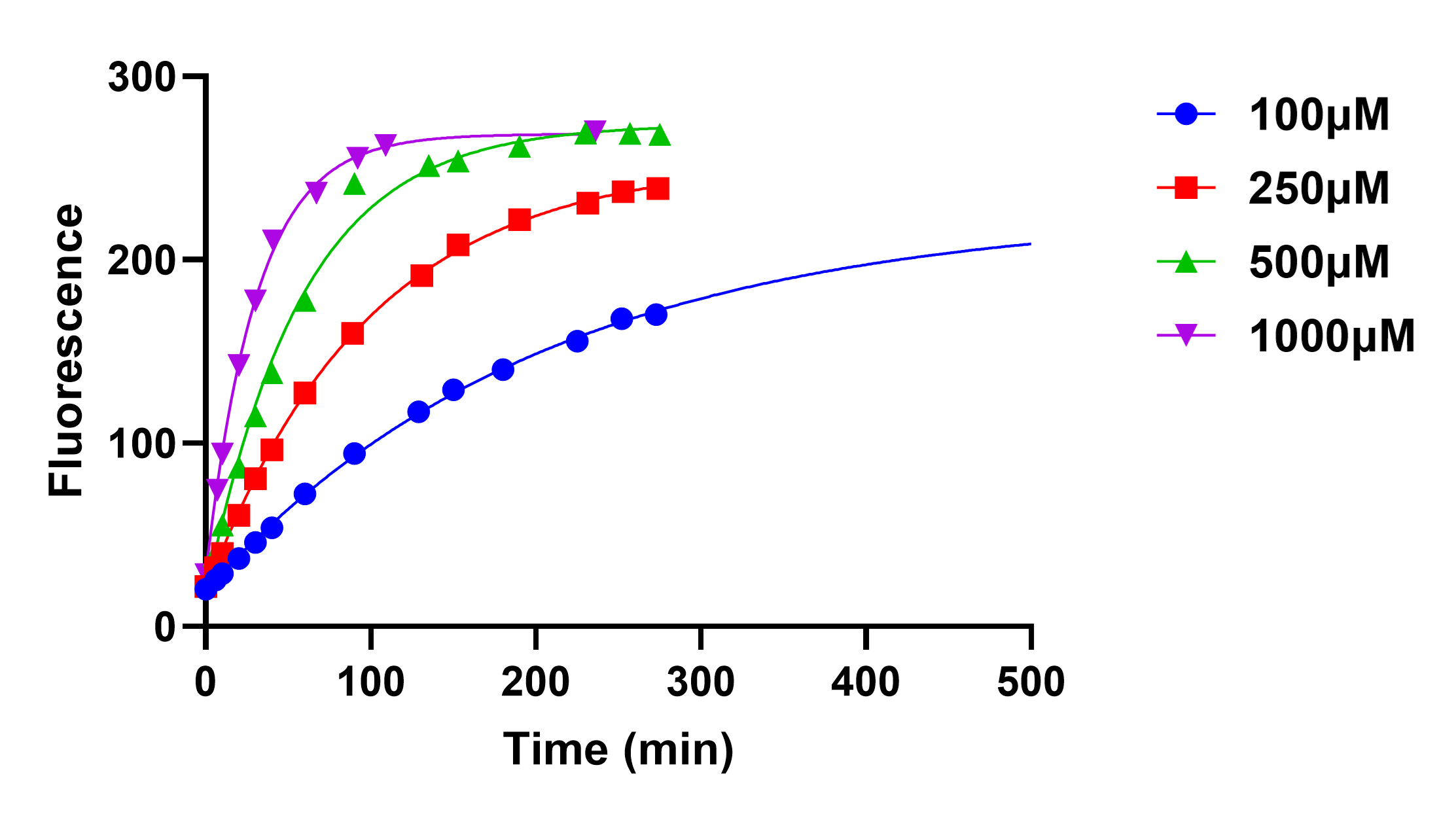
最后对$k_{\text{obs}}$做线性回归，得到此反应的${k_2}$。

五. 酶促反应

1.中间复合物模型

虽然人们一开始没有建立起描述酶促反应的数学方程，但是已经通过实验测定出了酶促反应的速率-底物浓度曲线。

虽然人们不知道怎么用数学语言去描述这个曲线，但是可以很直观地看到：
当底物浓度较低，反应速率随底物浓度的增加而近似呈正比地上升，长得很像一级反应。
随着底物浓度的升高，反应速率不再随底物浓度呈正比上升，反应速率上升的幅度不断减缓。
继续加大底物浓度至过量，反应速率不再上升，长得很像零级反应。此时即为酶的活性位点达到饱和。

根据实验现象，有人提出了“中间复合物模型”：在酶促反应中，酶与底物结合后会先形成一个不稳定的中间复合物。这个中间复合物既可以解离回酶和底物，也可以进一步完成酶促反应，释放出产物和酶。对于单底物不可逆酶促反应，其化学表达式如下。
$$ \text{E} + \text{S} \overset{k_1}{\underset{k_2}{\rightleftharpoons}} \text{ES} \xrightarrow{k_3} \text{E} + \text{P} $$ 其中$\text{E}$表示游离状态下的酶(Enzyme)，而$\text{S}$为反应底物(Substrate)，$\text{ES}$为中间复合物，$\text{P}$为产物(Product)。${k_1}$，${k_2}$和${k_3}$分别是结合、解离和催化反应这三个过程的速率常数。

2.快速平衡模型

为了描述单底物不可逆酶促反应的动力学方程，Michaelis和Menten（这两位就是米氏方程中的“米氏”，MM方程中的“MM”）在中间复合物模型的基础上，进一步提出了快速平衡模型。
快速平衡模型假设，$ \text{E} + \text{S} \rightleftharpoons \text{ES} $这一过程非常快，而后一步的催化反应要比它慢得多，即${k_2} \gg {k_3}$，$\text{ES}$生成为$\text{P}$的速率不足以破坏$\text{E}$和$\text{S}$与$\text{ES}$之间的平衡。
这一假设看上去是颇有道理的，$\text{ES}$的产生和解离，这是个物理过程，比后面$\text{ES}$生成$\text{P}$这个化学过程要快，似乎没什么不妥。

下面基于快速平衡模型，开始推导酶促反应动力学方程。
为了后面说事儿方便，定义以下参数。
$$\text{最大速率} \quad r_{\max} = k_3 [\text{E}_{\text{total}}]$$ $$ \text{解离常数} \quad K_{\text{d}} = \frac{k_2}{k_1} $$ $$\text{米氏常数} \quad K_{\text{m}} = \frac{k_2 + k_3}{k_1} $$ 最大速率$r_{\max}$很好理解。当全部的$\text{E}$，也就是$\text{E}_{\text{total}}$，都形成$\text{ES}$时，也就是所有$\text{E}$都火力全开进行酶促反应时，此时的速率$k_3 [\text{E}_{\text{total}}]$当然就是最大速率。

解离常数(Dissociation constant)$K_{\text{d}}$反映的是化合物对靶标的亲和力大小，值越小亲和力越强。这个常数与后面的催化反应过程没有任何关系，与什么快速不快速平衡的模型也没有任何关系。只要是个能跟酶活位点特异性结合的化合物，那它就一定有一个自己的$K_{\text{d}}$。
我一开始感到奇怪，为什么大家都用解离常数来描述化合物对酶的亲和力，而且还是用“值越小亲和力越强”这么拧巴的方式来描述？为什么不直接用${k_1}$除以${k_2}$这个更加直观的参数，而是倒过来使用呢？后来我知道，小分子药物对靶标的亲和力往往特别强，$K_{\text{d}}$的数值能达到nM级别。要是倒过来计算的话，这个数值就上天了，显然不适合传播和交流。在后面的推导中也可以看到，$K_{\text{d}}$这个参数在描述酶促反应中有着更加深刻的意义。

米氏常数(Michaelis-Menten constant)$K_{\text{m}}$将上述酶促反应模型中的三个速率常数联系在一起。对于一个酶促反应来说，$K_{\text{m}}$是它的“本征”属性、“内廪”属性。在后面的推导中也可以看到，$K_{\text{m}}$这个参数在描述酶促反应中有着更加深刻的意义。

现在真的要开始推导了。
我们对反应速率很感兴趣。对于任意单底物不可逆酶促反应，其反应速率总是
$$r = k_3 [\text{ES}], \quad [\text{ES}] \text{ is hard to know} $$ 可是前面也提过，$\text{ES}$是个不稳定的中间复合物，它的浓度并不容易测定，所以要通过其他易测量的参数来间接表示。
基于E与S的结合和解离的快速平衡，即结合速率等于解离速率，就可以得到E和S的浓度与ES的浓度的关系。
$$k_1 [\text{E}][\text{S}] = k_2 [\text{ES}]$$ 跑得了和尚跑不了庙，不管是游离的$\text{E}$还是形成复合物的$\text{ES}$，反正体系中酶的总量是固定的。这样一来，$\text{ES}$的浓度就可以用总的酶浓度$[\text{E}_{\text{total}}]$和底物的浓度$[\text{I}]$表示出来了。
$$ [\text{ES}] = \frac{k_1}{k_2} [\text{E}][\text{S}] $$ $$ [\text{ES}] + [\text{E}] = [\text{E}_{\text{total}}], \quad [\text{E}_{\text{total}}] \text{ is constant} $$ $$ [\text{ES}] = \frac{[\text{E}_{\text{total}}] [\text{S}]}{\frac{k_2}{k_1} + [\text{S}]} $$ 把$[{\text{ES}}]$代回到最开始的速率方程里，可以发现$k_3 [\text{E}_{\text{total}}]$刚好就是我们定义的$r_{\max}$，下面的$\frac{k_2}{k_1}$刚好就是我们定义的$k_{\text{d}}$。
$$r = k_3 [\text{ES}] = \frac{k_3 [\text{E}_{\text{total}}] [\text{S}]}{\frac{k_2}{k_1} + [\text{S}]} = \frac{r_{\max} [\text{S}]}{K_{\text{d}} + [\text{S}]}
$$ 这就是著名的米氏动力学方程。
当$[\text{S}]$极大的时候，速率无限趋近于$r_{\max}$。
当$[\text{S}]$极小的时候，速率近似与$[\text{S}]$成正比。
当$[\text{S}]$恰好等于$k_{\text{d}}$的时候，反应速率刚好是最大速率的一半。
米氏方程可以很贴切地描述实验现象。
顺带一提，在快速平衡模型中，$K_{\text{d}}$与$K_{\text{m}}$是近似相等的。
$$k_2 \gg k_3, \quad K_{\text{d}} = \frac{k_2}{k_1} = \frac{k_2 + k_3}{k_1} = K_{\text{m}} $$在后面会进一步讨论二者的区别与联系。

3.稳态模型

快速平衡模型在解释酶促反应的动力学机理上取得了重大突破，但是其假设并不是毫无问题的。我们知道酶促反应具有高效性，${k_3}$实际上应该是不低的，没道理认为对于所有酶促反应都有$k_2 \gg k_3$。后人对此进行修正，提出了酶促反应的稳态理论。
稳态模型假设，不管${k_2}$和${k_3}$之间到底是什么关系，反正在酶促反应过程中，ES的浓度总是恒定不变的。
基于此设定，再次推导酶促反应动力学方程。
ES的浓度不变，也就是它的生成速率$r_f$和消耗速率$r_d$相等。所以可以很轻松地得到
$$ r_f = r_d $$ $$ r_f = k_1 [\text{E}] [\text{S}] $$ $$r_d = k_2 [\text{ES}] + k_3 [\text{ES}] $$ $$[\text{ES}] = \frac{k_1}{k_2 + k_3} \cdot [\text{E}] [\text{S}] $$ 我们再一次地用$[\text{E}]$和$[\text{S}]$表示出了$[\text{ES}]$。而且可以看到，它长得跟快速平衡模型中很像。
后面的步骤就是照和尚画瓢了，利用酶总量守恒，求解$[\text{ES}]$，得到速率方程。
$$r = \frac{r_{\max} [\text{S}]}{K_{\text{m}} + [\text{S}]} $$ 这就是稳态模型下的米氏动力学方程，其数学形式与快速平衡模型下完全相同。
对于酶促反应，稳态模型的假设比快速平衡模型的假设更有普适性，前者的约束条件更“弱”一些。或者说，快速平衡模型实际上只是稳态模型下的一个特殊情况。
对于酶促反应，$K_{\text{m}}$才是最本征的，最能体现整个反应本质的那个参数。

对于$K_{\text{m}}$的具体实验测定，比较古典的做派是先测定不同底物浓度下的反应速率，然后将米氏方程两边取倒数，使其线性化，然后进行拟合。不过得益于计算机的发展，我们直接把测到的数据输入进Prism之类的软件里，选择米氏模型就能完成拟合。

例：Glutamate carboxypeptidase II(GCPII)可以将司谷氨酸(NAAG)水解为N-天冬氨酸(NAA)和谷氨酸(Glu)。试测定此反应的$K_{\text{m}}$。

尽管瞬时的反应速率并不容易直接测量，但我们可以设置一小段时间，将这一小段时间内的平均反应速率当作体系在当前底物浓度下的反应速率。
注意到底物和产物都没有较强的吸收波段和荧光发射，所以可以使用邻苯二甲醛(OPA)作为游离氨基的检测试剂来间接反映产物浓度。OPA与游离的一级胺和巯基共同作用可以快速生成具有荧光的物质。
将不同浓度的NAAG与固定浓度的GCPII孵育相同时间，然后加入OPA检测试剂，测定对应的荧光强度。
把测得的数据粘贴到Prism中，Analysis → Nonlinear regression → Enzyme kinetics - Velocity as a function of substrate → Michaelis-Menten，即可拟合得到$K_{\text{m}}$。

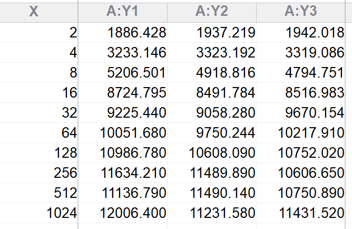
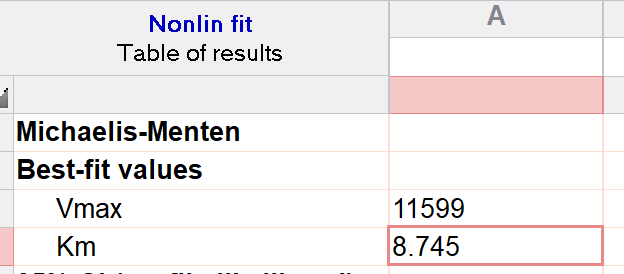
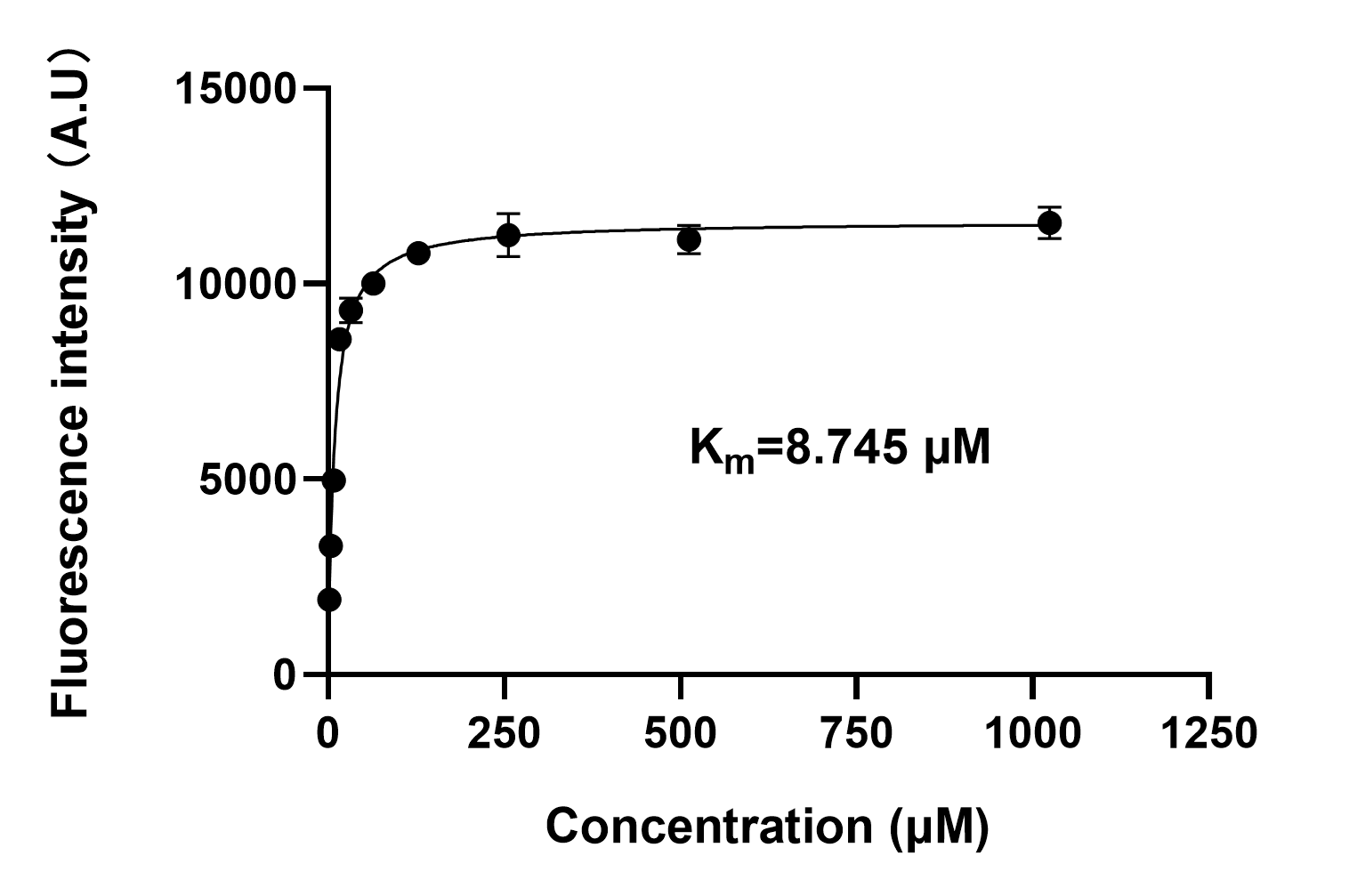
实验测得，NAAG对GCPII的$K_{\text{m}}$为8.745μM。

参考阅读：
Prism曲线拟合指南 方程：Michaelis-Menten模型

六. 有竞争性抑制剂参与时的酶促反应

对于酶促反应，人们也很关心抑制剂的设计与开发。抑制剂可以卡在与底物相同的活性口袋里，但是并不会被催化分解，只是单纯地与底物竞争性结合，降低酶的活性。
$$ \text{E} + \text{S} \overset{k_1}{\underset{k_2}{\rightleftharpoons}} \text{ES} \xrightarrow{k_3} \text{E} + \text{P} $$ $$\text{E} + \text{I} \overset{k_5}{\underset{k_6}{\rightleftharpoons}} \text{EI}$$其中$\text{I}$表示酶的抑制剂(Inhibitor)，$\text{EI}$为$\text{E}$与$\text{I}$形成的无活性的中间复合物。${k_5}$和${k_6}$分别是$\text{E}$与$\text{I}$的结合和解离过程的速率常数。

有抑制剂存在的情况下，体系中会额外多一个抑制剂与酶结合与解离的过程。
对于抑制剂来说，它也有它自己的解离常数$K_{\text{d}}$。抑制剂的$K_{\text{d}}$反映了抑制剂对酶的结合能力。在理想情况下，$K_{\text{d}}$就是所谓的$K_{\text{i}}$。抑制剂$\text{I}$的$K_{\text{d}}$嘛，那不就是$K_{\text{i}}$。但实际上二者并不等同，后面会详细分析。
$$ K_{\text{d}} = \frac{k_6}{k_5} = K_{\text{i}} \quad (\text{ideally}) $$ 在这种情况下如何描述反应速率呢。思路和前面一样，仍然是利用酶总量守恒和稳态模型来求解中间复合物ES的浓度。

酶总量守恒，有
$$ [\text{E}] + [\text{ES}] + [\text{EI}] = [\text{E}_{\text{total}}] $$ 把$[\text{E}]$和$[\text{EI}]$用$[\text{ES}]$表示出来，然后合并、移项就可以解得$[\text{ES}]$。

$[\text{ES}]$的生成速率与消耗速率相等，有
$$ k_1 [\text{E}][\text{S}] = k_2 [\text{ES}] + k_3 [\text{ES}] \quad \Rightarrow \quad [\text{E}] = \frac{k_2 + k_3}{k_1} \cdot \frac{[\text{ES}]}{[\text{S}]} = \frac{K_{\text{m}} [\text{ES}]}{[\text{S}]} $$ $[\text{EI}]$的生成速率与消耗速率相等，有
$$ k_5 [\text{E}][\text{I}] = k_6 [\text{E}][\text{I}] \quad \Rightarrow \quad [\text{EI}] = \frac{k_5}{k_6} [\text{E}][\text{I}] = \frac{K_{\text{m}} [\text{ES}][\text{I}]}{K_{\text{i}} [\text{S}]} $$

代入到酶守恒方程里，一通折腾，就可以得到有竞争性抑制剂存在时的酶促反应速率方程。
$$ \frac{K_{\text{m}} [\text{ES}]}{[\text{S}]} + [\text{ES}] + \frac{K_{\text{m}} [\text{ES}][\text{I}]}{K_{\text{i}} [\text{S}]} = [\text{E}_{\text{total}}] $$ $$[\text{ES}] = \frac{[\text{E}_{\text{total}}] [\text{S}]}{K_{\text{m}} (1 + \frac{[\text{I}]}{K_{\text{i}}}) + [\text{S}]} $$ $$r_{\text{withI}} = k_3 [\text{ES}] = \frac{r_{\text{max}} [\text{S}]}{K_{\text{m}} (1 + \frac{[\text{I}]}{K_{\text{i}}}) + [\text{S}]} $$ 可以看到，在抑制剂竞争结合时，反应速率方程的形式与前面仍然非常相似，只不过多了一个抑制剂的项。此时的速率方程也非常好理解，
$[\text{I}]$特别大的时候，分母也很大，反应速率趋近于0，代表酶活位点几乎都被抑制剂卡死了。
$[\text{I}]$特别小的时候，分母与原始的速率方程相比变化很小，反应速率近似不变，代表抑制剂几乎没怎么干扰酶促反应。

有抑制剂存在的情况下，我们格外关注一个参数，$IC_{50}$，即半数抑制浓度，它表示需要多少浓度的抑制剂才能抑制50%的酶活性。
下面进行一段关于$IC_{50}$的数学推导。

有抑制剂时，反应速率为
$$r_{\text{withI}} = k_3 [\text{ES}] = \frac{r_{\text{max}} [\text{S}]}{K_{\text{m}} (1 + \frac{[\text{I}]}{K_{\text{i}}}) + [\text{S}]} $$ 无抑制剂时，反应速率为
$$ r_{\text{noI}} = \frac{r_{\max} [\text{S}]}{K_{\text{m}} + [\text{S}]} $$ 当二者的比值为$\frac{1}{2}$，此时的$[\text{I}]$就是$IC_{50}$。一通移项，就可以得到$IC_{50}$与$K_{\text{i}}$之间的对应关系。

$$\frac{r_{\text{withI}}}{r_{\text{no I}}} = \frac{K_{\text{m}} + [\text{S}]}{K_{\text{m}} \left( 1 + \frac{IC_{50}}{K_{\text{i}}} \right) + [\text{S}]} = \frac{1}{2}$$ $$K_{\text{m}} \cdot \frac{IC_{50}}{K_{\text{i}}} = K_{\text{m}} + [\text{S}]$$ $$ K_{\text{i}} = \frac{IC_{50}}{1 + \frac{[\text{S}]}{K_{\text{m}}}}$$ 可以看到，$K_{\text{i}}$与$IC_{50}$密切相关。这是理所当然的。二者都反映了抑制剂对酶的结合能力。
如果$IC_{50}$特别小，对应着$K_{\text{i}}$也特别小，也就是抑制剂与酶的结合能力特别强，一点点的抑制剂就可以抑制50%的酶活性。
如果$IC_{50}$特别大，对应着$K_{\text{i}}$也特别大，也就是抑制剂与酶的结合能力特别弱，非常多的抑制剂才可以抑制50%的酶活性。

$IC_{50}$是一个实验上很直观，很容易测定的东西。我们设置不同浓度的抑制剂，与固定浓度的酶和底物一起孵育，分别测定对应的抑制效果，将抑制剂浓度与抑制效果作图，很容易地就可以得到我们熟悉的S型剂量反应(Sigmoidal dose-response)曲线。其数学形式如下。

$$ \begin{align} \frac{r_{\text{withI}}}{r_{\text{no I}}} &= \frac{K_{\text{m}} + [\text{S}]}{K_{\text{m}} + [\text{S}] + \frac{K_{\text{m}}}{K_{\text{i}}} [\text{I}]} \\ &= \frac{K_{\text{m}} + [\text{S}]}{K_{\text{m}} + [\text{S}] + \frac{K_{\text{m}} + [\text{S}]}{IC_{50}} \cdot [\text{I}] } \\ &= \frac{1}{1 + \frac{[\text{I}]}{IC_{50}}} \\ &= \frac{1}{1 + 10^{\lg[\text{I}]-\lg{IC_{50}}}} \end{align} $$

这就是我们熟悉的S型曲线的数学表达式。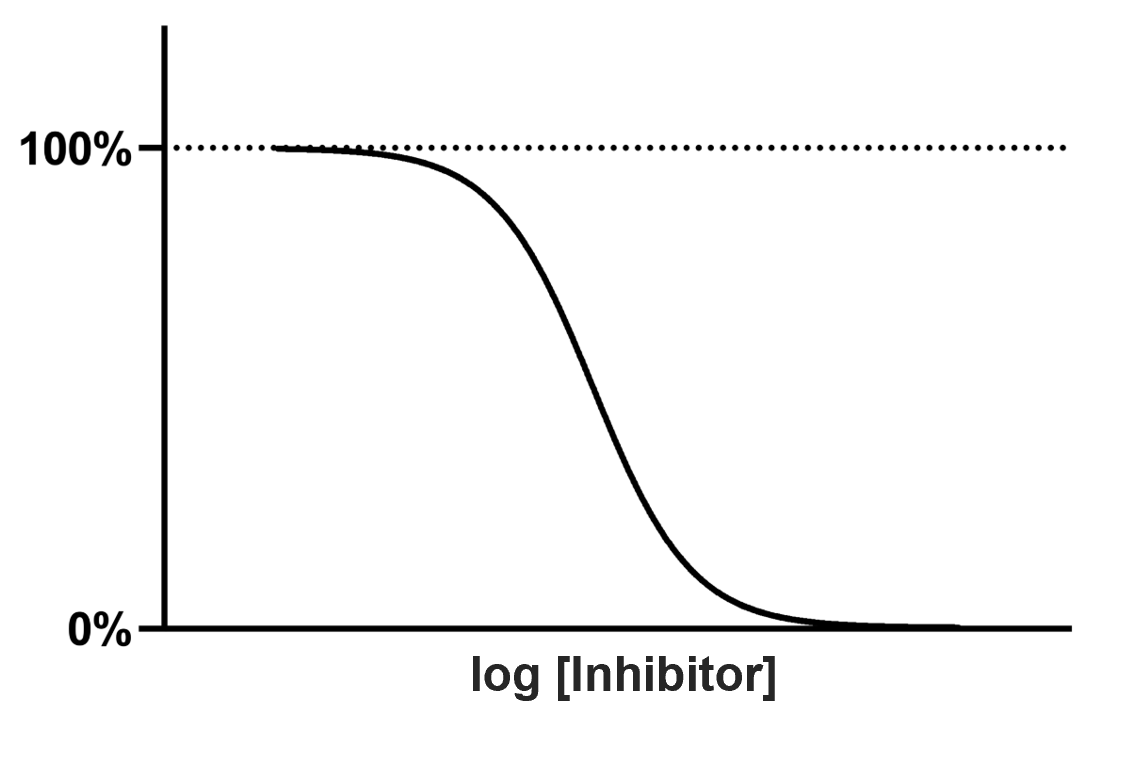

当曲线下降到50%时，对应的抑制剂浓度即为$IC_{50}$。同理，$IC_{75}$，$IC_{90}$等参数也可以利用此曲线求得。

至此，我们完成了最基础的酶促反应动力学模型的数学推导。下面针对刚才提到的几个概念进行辨析。

1.对于某一对酶和底物，其米氏常数$K_{\text{m}}$与解离常数$K_{\text{d}}$的关系

$$ \text{E} + \text{S} \overset{k_1}{\underset{k_2}{\rightleftharpoons}} \text{ES} \xrightarrow{k_3} \text{E} + \text{P} $$ $$ \text{解离常数} \quad K_{\text{d}} = \frac{k_2}{k_1} $$ $$\text{米氏常数} \quad K_{\text{m}} = \frac{k_2 + k_3}{k_1} $$ 对于某底物与某酶的酶促反应，在“测定不同底物浓度下的反应速率，然后拟合米氏方程”的动力学实验中，我们真实测得的就是米氏常数$K_{\text{m}}$。只有当快速平衡的假设成立时，$K_{\text{d}}$才近似等于$K_{\text{m}}$。但是事实上，我们并不知道$k_2$与$k_3$的关系究竟如何，我们此时确切知道的只有$K_{\text{m}}$，所以$K_{\text{m}}$就是$K_{\text{m}}$，$K_{\text{d}}$就是$K_{\text{d}}$，没有更多信息时不能将二者混为一谈。

2.对于某一对酶和抑制剂，其半数抑制浓度$IC_{50}$与抑制常数$K_{\text{i}}$的关系

$$ K_{\text{i}} = \frac{IC_{50}}{1 + \frac{[\text{S}]}{K_{\text{m}}}}$$ $IC_{50}$是我们真切测定得到的半数抑制浓度数值，但是很显然，它会受到酶浓度和底物浓度的影响。比如酶浓度和底物浓度很高，当然需要很多抑制剂才能把酶活性压到50%。
对于某一对酶和抑制剂，$IC_{50}$是可变的，而${K_{\text{i}}}$则不受酶浓度和底物浓度的干扰，它才是这个抑制剂的所谓的“本征”属性、“内廪”属性，更接近抑制剂的“本质”。
这很像在讨论二级反应时，表观速率常数$k_{\text{obs}}$与二级反应速率常数$k_2$之间的关系。

3.对于某一对酶和抑制剂，其抑制常数$K_{\text{i}}$与解离常数$K_{\text{d}}$的关系

$$ K_{\text{i}} = \frac{IC_{50}}{1 + \frac{[\text{S}]}{K_{\text{m}}}}$$ 前面提到过“在理想情况下，$K_{\text{d}}$就是所谓的$K_{\text{i}}$，但实际上二者并不等同”。这个“理想情况”，就是“没有其它物质与该抑制剂进行竞争性结合”。
$K_{\text{d}}$反映的是干干净净的抑制剂与酶的结合能力，而我们测定的$K_{\text{i}}$，是在有底物存在的情况下进行竞争性结合实验得到的。
酶的总量一定时，若想达到50%的酶被抑制剂$\text{I}$结合，必定比无底物$\text{S}$竞争时需要的抑制剂$\text{I}$更多，所以我们真实测得的$K_{\text{i}}$实际上会比$K_{\text{d}}$要大一点。
对于$K_{\text{d}}$，实验上可以通过等温滴定量热法(Isothermal titration calorimetry)或表面等离子共振(Surface plasmon resonance)等方式测得。
显然，通过竞争性实验得到的$K_{\text{i}}$是无法与通过物理手段得到的$K_{\text{d}}$混为一谈的。

例：化合物ZJ43是GCPII的高效抑制剂。试测定其$K_{\text{i}}$。

在已知底物NAAG的$K_{\text{m}}$的情况下，我们可以固定NAAG和GCPII的浓度不变，将不同浓度的ZJ43与其共孵育，得到抑制效率与ZJ43浓度的关系。
把测得的数据粘贴到Prism中，Analysis → Nonlinear regression → Classic equations from prior versions of Prism → Sigmoidal dose-response → 在output选项卡中输入已经测得的KD与当前酶浓度，即可拟合得到$K_{\text{i}}$。

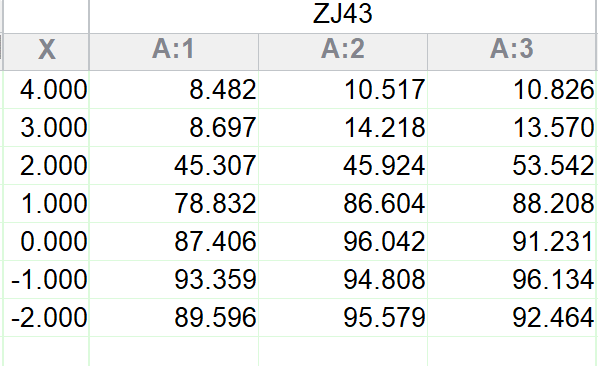
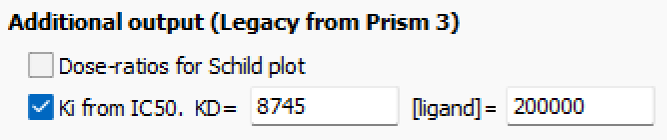
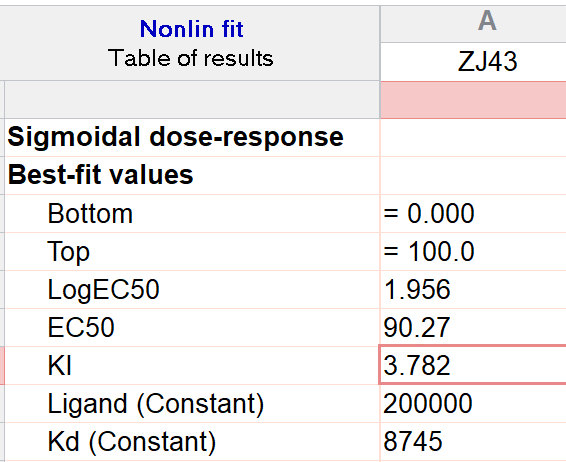
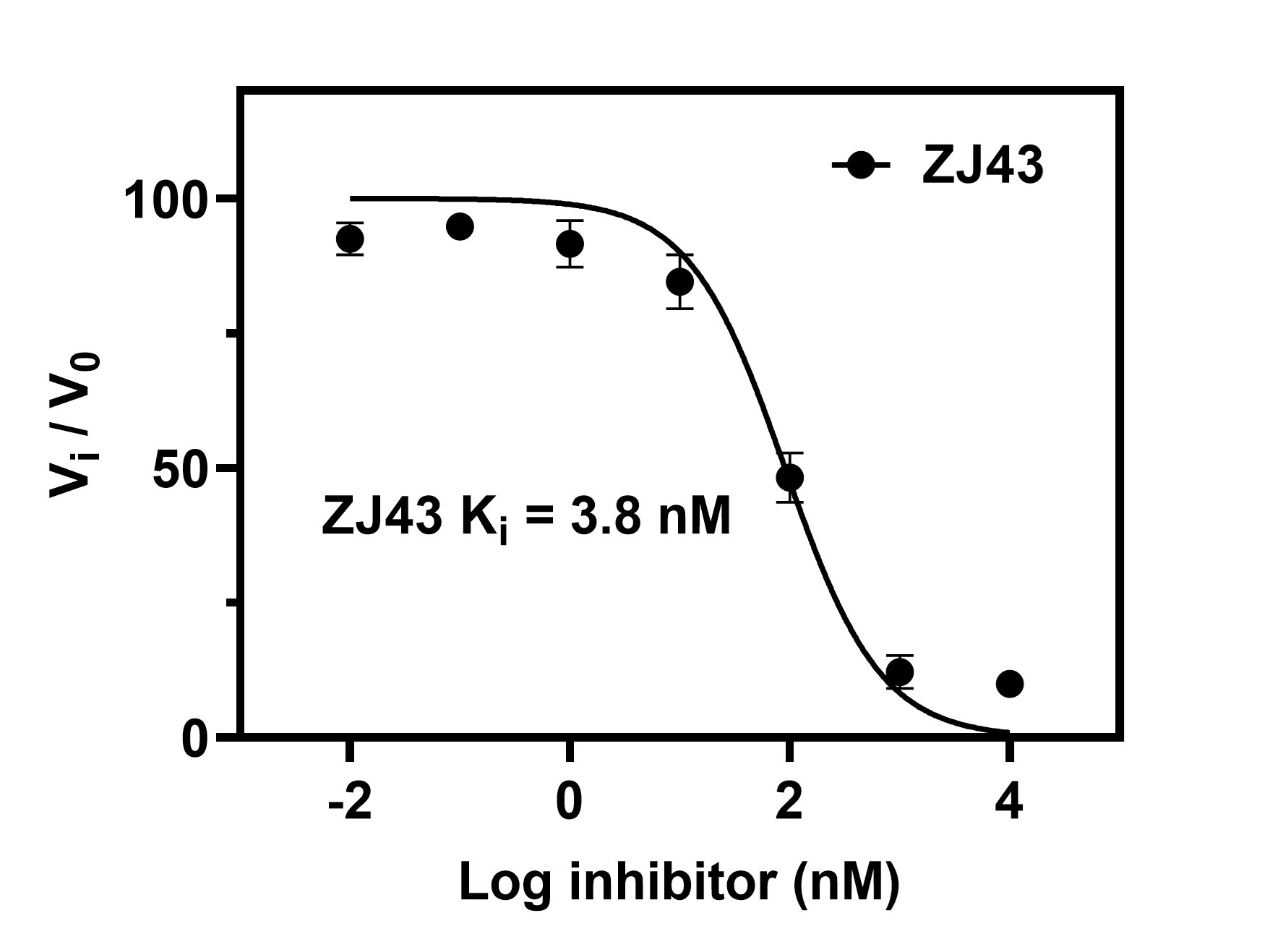
实验测得，ZJ43的$K_{\text{i}}$为3.8nM。
吐槽：可以看到，Prism官方其实也不怎么区分$K_{\text{m}}$和$K_{\text{d}}$，不过无所谓了，我们自己能弄清楚是怎么回事儿就行了。

参考阅读：
Prism曲线拟合指南 方程：Sigmoidal剂量反应

七. 后记

本文脱胎于课堂展示，所以充满口语化的表述。
本文做了大量避重就轻的推导。尤其是在酶促反应动力学部分，忽略了产物对酶的竞争性结合，酶促反应过程第二步的逆反应，激动剂，拮抗剂、变构调节、非竞争性抑制等过程，因为笔者自己也还没弄明白。